On February 17th, 2019, I participated in a mathematical bookbinding workshop to learn about the history and process of bookbinding.
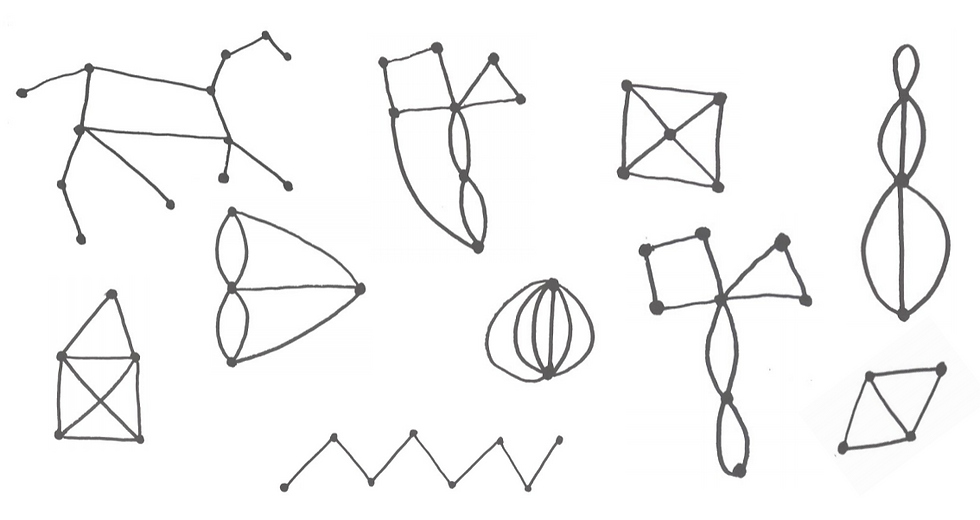
The workshop started with us trying to complete graph puzzles, as seen to the left. The task was to start at one vertex and try to trace all of the edges of each graph without lifting our pen. We were told that math could be used to quickly figure this out. Leonhard Euler said to count all the edges connected to each vertex, and call that number the “degree” of the vertex. If the degree of all vertices is even, there is a route through all the edges that returns to its starting point, which is called an Euler circuit. If the degree of exactly two vertices is odd, there is a route through all the edges that starts at one of the odd vertices and ends at the other, which is called an Euler path. If there is any other number of odd-degree vertices, it can't be done.
Natalie Freed, the workshop lead, explained how this information could be used for bookbinding. She said, "Since in a traditional stab book every edge is doubled (for the front
and back stitches), every hole will always have an even number of connections reaching it. So there will always be an Euler circuit, and thus always a way to stitch it." In other words, I needed to make sure that the number of degrees of all vertices in my pattern was even.
I tried to create my own pattern, but I was running out of time, so I looked online for patterns. I found a lotus flower pattern that I wanted to try, which can be found here. I used graph paper to plot the 36 holes, and then I used a drill to create the holes through my book. Then, the stitching process began. The website told me exactly how to stitch it, so it was very easy to do.
Reflection
I enjoyed participating in this workshop because I love math and crafts. I would like to see if I could have my future students do this too. They could create their own patterns on Geogebra and print them out.
I would like to create my own pattern the next time that I do this.
References
Natalie Freed, Becca Rose Glowacki https://drive.google.com/file/d/0B5Wi9harvTDXODdrME16VzVpbGs/view